Learning Outcomes
i. Comprehend the concepts of nodes and antinodes in stationary waves, recognizing their distinct characteristics and positions within the wave pattern.
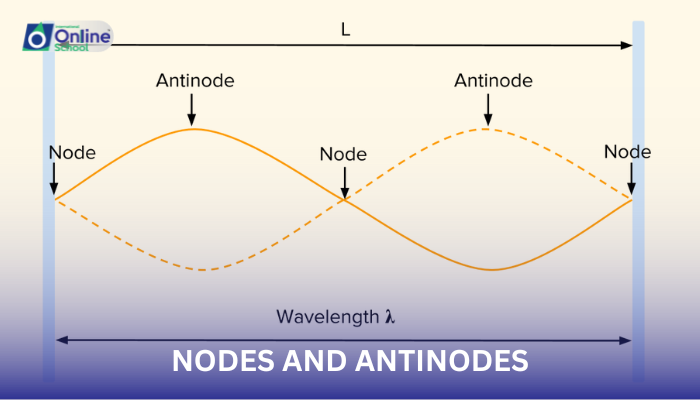
ii. Define nodes as points in a stationary wave where the displacement is always zero, creating dark spots in the graphical representation.
iii. Define antinodes as points in a stationary wave where the displacement is maximum, creating bright spots in the graphical representation.
iv. Analyze the relationship between nodes, antinodes, and the wavelength of the stationary wave, understanding that the wavelength is the distance between two consecutive nodes or antinodes.
v. Identify real-world applications of nodes and antinodes, such as musical instruments and resonant cavities.
Introduction
As we observe the rhythmic vibrations of a plucked guitar string or the gentle lapping of waves against a shore, we witness the captivating phenomenon of stationary waves. This lesson delves into the realm of wave physics, exploring the intricate interplay of nodes and antinodes, the fundamental building blocks of these fascinating waves.
i. Nodes: Points of Stillness in the Symphony of Waves
Nodes are points in a stationary wave where the displacement of the medium is always zero. These points appear as dark spots in the graphical representation of the wave pattern, indicating that the medium remains undisturbed at these locations. Nodes arise from the destructive interference of two waves traveling in opposite directions.
ii. Antinodes: Points of Maximum Oscillation
Antinodes are points in a stationary wave where the displacement of the medium is maximum. These points appear as bright spots in the graphical representation of the wave pattern, indicating that the medium oscillates with maximum amplitude at these locations. Antinodes also arise from the interference of two waves, but in this case, the waves interfere constructively, producing the maximum displacement.
iii. A Symphony of Wavelengths: The Connection Between Nodes and Antinodes
The wavelength of a stationary wave is the distance between two consecutive nodes or antinodes. This relationship highlights the periodicity of the wave pattern, with nodes and antinodes repeating at regular intervals along the wave's propagation.
iv. Real-World Applications: A Symphony of Nodes and Antinodes in Action
Nodes and antinodes play crucial roles in various real-world applications:
Musical Instruments: The vibrations of strings, air columns, and membranes in musical instruments create standing waves, with nodes and antinodes determining the pitch and timbre of the produced sounds.
Resonant Cavities: Nodes and antinodes are utilized in resonant cavities, such as the bodies of musical instruments and the chambers of loudspeakers, to enhance specific frequencies and create desired sound qualities.
Nodes and antinodes, with their distinct characteristics and their relationship to the wavelength of stationary waves, provide a fundamental understanding of the behavior of these captivating waves. From the musical notes we hear when playing an instrument to the resonant tones of a cathedral, nodes and antinodes shape our auditory experiences and play a pivotal role in diverse applications. As we continue to explore the realm of wave physics, we gain deeper insights into the intricate workings of stationary waves, unraveling the secrets of their behavior and their diverse manifestations in nature and technology.